Действия описаны в хронологическом порядке.
По сути формула \eqref{eq:new_speed} описывает фильтр нижних частот, вносящий задержку в исходный сигнал \( {\upsilon'}_e \left(d\right) \). Формулу \eqref{eq:new_speed} можно представить в виде:
\begin{equation}\label{eq:new_speed_as_filter} {a'}_t = \frac{a_t - {a'}_{t-1}}{k} + {a'}_{t-1} \end{equation}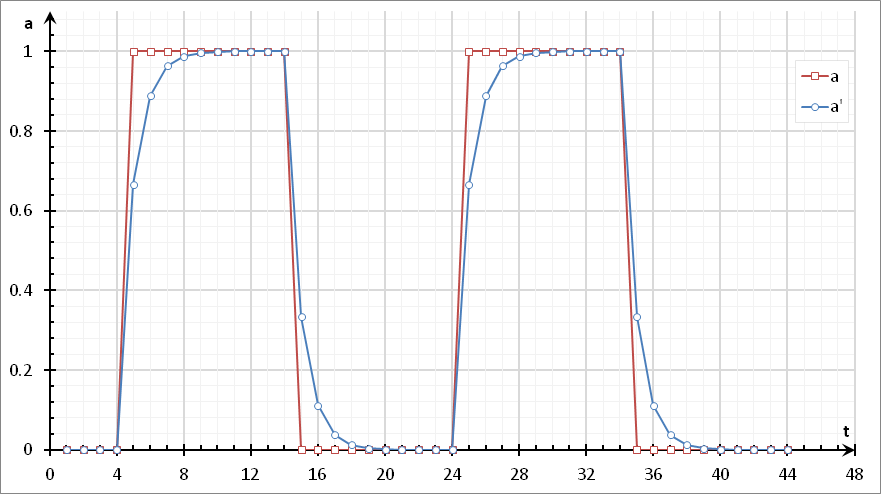
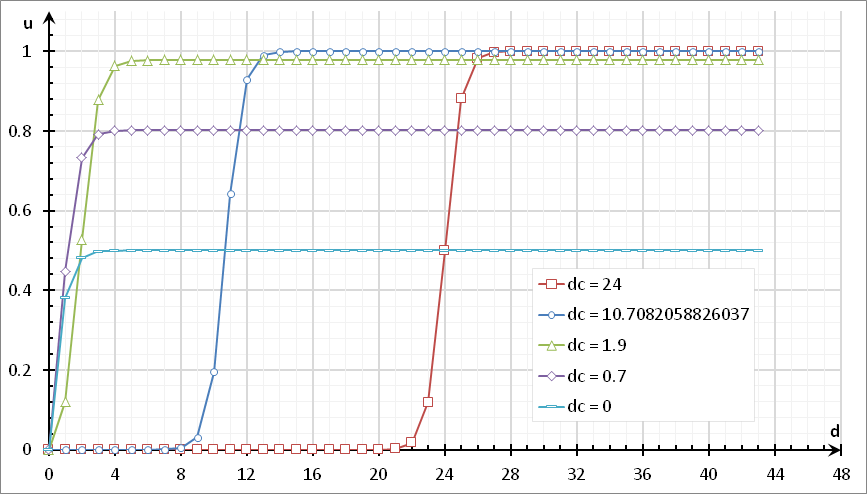
Определим, выгоду (точность и скорость вычисления) от аналитического решения формул \eqref{eq:new_speed} и \eqref{eq:opt_speed}.
Для этого объединим две формулы в одну:
Положим \( \mu \left( t \right) = e^{\int \frac{1}{\tau} dt} = e^{{t}/{\tau}} \).
Умножим обе стороны \eqref{eq:analit_speed_2} на \( \mu \left( t \right) \):
\begin{equation}\label{eq:analit_speed_3} e^{{t}/{\tau}} \frac{d \upsilon_n \( t \) }{d t} + \frac{ e^{{t}/{\tau}} \upsilon_n \( t \) }{\tau} = \frac{ e^{{t}/{\tau}} \upsilon_0 \( \tanh \( d-d_c \) +\tanh \( d_c \) \) }{2\tau}. \end{equation}Произведем замену \( { e^{{t}/{\tau}} }/{\tau} = \frac{d}{dt} \left( e^{{t}/{\tau}} \right) \):
\begin{equation}\label{eq:analit_speed_4} e^{{t}/{\tau}} \frac{d \upsilon_n \( t \) }{d t} + \frac{d}{dt} \( e^{{t}/{\tau}} \) \upsilon_n \( t \) = \frac{ e^{{t}/{\tau}} \upsilon_0 \( \tanh \( d-d_c \) +\tanh \( d_c \) \) }{2\tau}. \end{equation}Применим обратное тождество Лейбница \( g\frac{df}{dt} + f\frac{dg}{dt} = \frac{d}{dt} \left( f \cdot g \right) \):
\begin{equation}\label{eq:analit_speed_5} \frac{d}{dt} \( e^{{t}/{\tau}} \cdot \upsilon_n \( t \) \) = \frac{ e^{{t}/{\tau}} \upsilon_0 \( \tanh \( d-d_c \) +\tanh \( d_c \) \) }{2\tau}. \end{equation}Интегрируем по \( t \):
\begin{equation}\label{eq:analit_speed_6} \int \frac{d}{dt} \( e^{{t}/{\tau}} \cdot \upsilon_n \( t \) \) dt = \int \frac{ e^{{t}/{\tau}} \upsilon_0 \( \tanh \( d-d_c \) +\tanh \( d_c \) \) }{2\tau} dt. \end{equation}Вычислим интегралы:
\begin{equation}\label{eq:analit_speed_7} e^{{t}/{\tau}} \cdot \upsilon_n \( t \) = \frac{ \int \( e^{{t}/{\tau}} \upsilon_0 \tanh \( d-d_c \) + e^{{t}/{\tau}} \upsilon_0 \tanh \( d_c \) \) dt }{2\tau} + с_1. \end{equation}Разделим обе стороны на \( \mu \left( t \right) \):
\begin{equation}\label{eq:analit_speed_8} \upsilon_n \( t \) = \frac{ \int \( e^{{t}/{\tau}} \upsilon_0 \tanh \( d-d_c \) + e^{{t}/{\tau}} \upsilon_0 \tanh \( d_c \) \) dt }{2\tau \cdot e^{{t}/{\tau}} } + \frac{с_1}{e^{{t}/{\tau}}},\\ \upsilon_n \( t \) = \frac{ \int e^{{t}/{\tau}} \upsilon_0 \tanh \( d-d_c \) dt + \int e^{{t}/{\tau}} \upsilon_0 \tanh \( d_c \) dt }{2\tau \cdot e^{{t}/{\tau}} } + \frac{с_1}{e^{{t}/{\tau}}}. \end{equation}Вычислим интеграл:
\begin{equation}\label{eq:analit_speed_9} \upsilon_n \( t \) = \frac{ \upsilon_0 \int e^{{t}/{\tau}} \tanh \( d-d_c \) dt + \tau \upsilon_0 \tanh \( d_c \) \cdot e^{{t}/{\tau}} + c_2 }{2\tau \cdot e^{{t}/{\tau}} } + \frac{с_1}{e^{{t}/{\tau}}},\\ \upsilon_n \( t \) = \frac{ \upsilon_0 \int e^{{t}/{\tau}} \tanh \( d-d_c \) dt }{2\tau \cdot e^{{t}/{\tau}} } + \frac{ \tau \upsilon_0 \tanh \( d_c \) \cdot e^{{t}/{\tau}} }{2\tau \cdot e^{{t}/{\tau}} } + \frac{c_2}{2\tau \cdot e^{{t}/{\tau}} } + \frac{с_1}{e^{{t}/{\tau}}}, \end{equation} \begin{equation}\label{eq:analit_speed_10} \upsilon_n \( t \) = \frac{ \upsilon_0 \int e^{{t}/{\tau}} \tanh \( d-d_c \) dt }{2\tau \cdot e^{{t}/{\tau}} } + \frac{ \upsilon_0 \tanh \( d_c \) }{2} + \frac{с_1}{e^{{t}/{\tau}}} + \frac{c_2}{2\tau \cdot e^{{t}/{\tau}} }. \end{equation}Оставшийся в формуле \eqref{eq:analit_speed_10} интеграл, предлагается решить одним из численных методов.
Определим сложность формулы как количество включений сложных для расчета функций.
Выделим из формулы \eqref{eq:analit_speed_10} сложные для расчета функции: \( \tanh() \), \( e^{{t}/{\tau}} \). Определим количество вычислений сложных функций, при расчете очередного значения \( \upsilon_n \left( t \right) \): \( \tanh() \) - (в зависимости от метода численного интегрирования); \( e^{{t}/{\tau}} \) - (2 + в зависимости от метода численного интегрирования).
Выделим из формулы \eqref{eq:analit_speed_1} сложные для расчета функции: \( \tanh() \). Определим количество вычислений сложных функций, при расчете очередного значения \( \upsilon_n \left( t \right) \): \( \tanh() \) - (в зависимости от метода численного интегрирования).
Из сравнения формул \eqref{eq:analit_speed_1} и \eqref{eq:analit_speed_10} видно, что в результате применения аналитического интегрирования к формуле \eqref{eq:analit_speed_1}, получилась более сложная для расчета формула \eqref{eq:analit_speed_10}. Увеличенная сложность вычислений может компенсироваться увеличенной точностью вычислений. Анализ точности вычислений не проводился.
Результаты анализа формулы \eqref{eq:opt_speed} и её графиков , показал, что вычислительно сложная функция \( \tanh() \) используется в качестве сигмоиды, и, в принципе, может быть заменена на любую другую сигмоидальную функцию. Для выбора оптимальной (с точки зрения вычислений) сигмоидальной функции, следует обратиться к области, в которой они нашли широкое применение. Эта область занимается построением искусственных нейронных сетей, причем функции, которые выполняет сигмоидальная функция в формуле \eqref{eq:opt_speed}, и в искусственных нейронных сетях - совпадают.
Так как функция \( \tanh() \) может быть представлена в виде:
\begin{equation}\label{eq:tanh} \tanh \( x \) = \frac{e^{2x}-1}{e^{2x}+1}, \end{equation}то также следует рассмотреть различные реализации вычисления степеней экспоненты (\( e^x \)).
Следующим шагом был анализ статей, описывающих ускоренные реализации гиперболического тангенса (\( \tanh() \)), и быстрого вычисления степеней экспоненты (\( e^x \)) [http://neuropro.ru/memo312.shtml, http://neuropro.ru/memo329.shtml, http://www.musicdsp.org/showone.php?id=222, http://stackoverflow.com/questions/10552280/fast-exp-calculation-possible-to-improve-accuracy-without-losing-too-much-perfo/10792321#10792321, http://martin.ankerl.com/2007/02/11/optimized-exponential-functions-for-java/, http://www.musicdsp.org/showone.php?id=178, http://stackoverflow.com/questions/6118028/fast-hyperbolic-tangent-approximation-in-javascript]. По завершению анализа было выбрано несколько ускоренных реализации функций, и составлен тест сравнения скорости реализаций.
inline float fastexp3(float x) //0.374s
{
return (6+x*(6+x*(3+x)))*0.16666666f;
}
inline float fastexp4(float x) //0.452s
{
return (24+x*(24+x*(12+x*(4+x))))*0.041666666f;
}
inline float fastexp5(float x) //0.530s
{
return (120+x*(120+x*(60+x*(20+x*(5+x)))))*0.0083333333f;
}
inline float fastexp6(float x) //0.624s
{
return 720+x*(720+x*(360+x*(120+x*(30+x*(6+x)))))*0.0013888888f;
}
inline float fastexp7(float x) //0.702s
{
return (5040+x*(5040+x*(2520+x*(840+x*(210+x*(42+x*(7+x)))))))*0.00019841269f;
}
inline float fastexp8(float x) //1.076s
{
return (40320+x*(40320+x*(20160+x*(6720+x*(1680+x*(336+x*(56+x*(8+x))))))))*2.4801587301e-5;
}
// http://www.musicdsp.org/showone.php?id=222
//exp(x)=exp(a)*exp(x-a), fastexp() is good (max error: ~0.45%) for 0 to ~7.5
inline float fastexp(const float x) //0.608s
{
if(x<2.5f) return 2.7182818f * fastexp5(x-1.f);
else if(x<5.f) return 33.115452f * fastexp5(x-3.5f);
else return 403.42879f * fastexp5(x-6.f);
}
// http://stackoverflow.com/questions/10552280/fast-exp-calculation-possible-to-improve-accuracy-without-losing-too-much-perfo/10792321#10792321
/* max. rel. error <= 1.73e-3 on [-87,88] */
inline float fast_exp(const float x) //0.577s
{
/*volatile*/ union {
float f;
unsigned int i;
} cvt;
/* exp(x) = 2^i * 2^f; i = floor(log2(e) * x), 0 <= f < 1 */
cvt.f=x*1.442695041f;
float fi=(int)cvt.f;
cvt.f-=fi;
if(cvt.f<0.f) fi-=1.f, cvt.f+=1.f;
cvt.f=(0.3371894346f*cvt.f + 0.657636276f)*cvt.f + 1.00172476f; /* compute 2^f */
cvt.i+=((int)fi)<<23; /* scale by 2^i*/ // *=1<<i
return cvt.f;
}
// http://martin.ankerl.com/2007/02/11/optimized-exponential-functions-for-java/
inline float fast_exp_min(float x) //1.014s
{
union{
double d;
struct{
int j, i;
} n;
} _eco;
return _eco.n.i = 1512775*(x) + 1072632447, _eco.d;
}
//=====================================================
// http://www.musicdsp.org/showone.php?id=178
inline float tanh2(float x) // 1.060s
{
x*=2;
float a=fabsf(x);
a=6+a*(6+a*(3+a));
return ((x<0)?-1:1)*(a-6)/(a+6);
}
// http://www.musicdsp.org/showone.php?id=178
inline float tanh2_min(float x) // 1.794s
{
x*=2;
return x/(fabsf(x)+3/(2+x*x));
}
// http://stackoverflow.com/questions/6118028/fast-hyperbolic-tangent-approximation-in-javascript
#ifdef __NVCC__
__device__ __forceinline__
#endif
inline float rational_tanh(const float x) // 0.982s - bestQ
{
#define _R_TANH_V 0
#if _R_TANH_V==0
return (x<-3.f) ? -1.f : ((x>3.f) ? 1.f : x*(27.f+x*x)/(27.f+9.f*x*x));
#elif _R_TANH_V==1
return ((x<-3.f)|(x>3.f)) ? copysignf(1.f,x) : x*(27.f+x*x)/(27.f+9.f*x*x);
#elif _R_TANH_V==2
const float q = copysignf(fminf(fabsf(x), 3.f), x);
return q*(27.f+q*q)/(27.f+9.f*q*q);
#endif
}
inline float tan_tanh(float x) // 1.138s
{
x = 2*fastexp(x);
return (x-1)/(x+1);
}
void test_approxmath()
{
float h0=0.25f, h1=0.25f, h2=0.25f, h3=0.25f;
for(int i=0; i<25000000; i++){
h0 /= A_EXP(h0+1.1f);
h1 /= A_EXP(h1+1.1f);
h2 /= A_EXP(h2+1.1f);
h3 /= A_EXP(h3+1.1f);
}
printf("%f\n", h0+h1+h2+h3);
} Результаты теста приведены рядом с описанием функций , время оригинальной ускоренной функции (включенной в библиотеку) составляет 2.589 секунд. Посмотрим на графики функций, и определим, какая из ускоренных функций находится ближе всего к оригинальной функции.
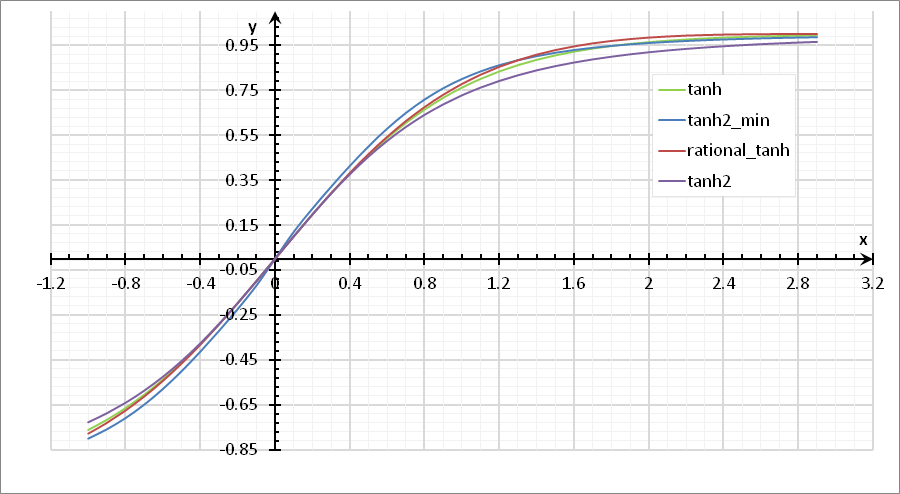
По совокупности качеств (скорость расчета, и близость к оригинальной функции) была выбранна функция rational_tanh().
Выбор метода численного интегрирования: Метод Рунге-Кутты с возможностью замены на Метод Рунге-Кутты-Кэша-Карпа [http://alglib.sources.ru/diffequations/rungekutta.php] (метод, изменяющий длину шага в зависимости от текущей оценки погрешности). Остальные идеи в файле "Labs/Васильеву/calc".
-пояснение синтаксиса.
Число машин равно числу вычислительных блоков. 4 машины.
Конец дороги задается положением "камня", т.н. автомобиля, который не двигается (не обрабатывается).
#include "approxmath.h"
// exp() is 1.092s
// tanhf() is 2.589s
#define A_EXP fast_exp
#define A_TANH rational_tanh
/*__declspec(align(16))*/
struct Car{
const float toSpeed = 5.f,
toDist = 5.f,
lenght = 1.f; // car: (end[lenght|y]>start)
float y;
float speed;
};
__declspec(vector (uniform(tRealx)))
inline float speed(float toSpeed, float toDist, float currentSpeed, float currentDist, float tRealx)
{
return (1.f/tRealx)*(toSpeed/2.f*(A_TANH(currentDist-toDist)+A_TANH(toDist)) - currentSpeed);
}
__declspec(vector (uniform(tIter)))
inline float distance(const Car &a, const Car &b, const float &aNewSpeed, const float &bNewSpeed, const float &tIter)
{
return (b.y-b.lenght + tIter*b.speed + 0.5f*(bNewSpeed*bNewSpeed - b.speed*b.speed)) - (a.y + tIter*a.speed + 0.5f*(aNewSpeed*aNewSpeed - a.speed*a.speed));
}
void calc_v2()
{
const float tRealx = 4.f;
const float tIter = 1.0f;
Car car[5] = {{150.f,0.f}/*<-stop*/, {3.f,0.f}, {2.f,0.f}, {1.f,0.f}, {0.f,0.f}};
for(int iter=0; iter<80000; iter++){
__declspec(align(16)) float k1[5]={0.f},k2[5]={0.f},k3[5]={0.f},k4[5]={0.f};
k1[1:4] = speed(car[1:4].toSpeed, car[1:4].toDist, car[1:4].speed , distance(car[1:4],car[0:4],car[1:4].speed ,car[0:4].speed ,0.f ), tRealx);
k2[1:4] = speed(car[1:4].toSpeed, car[1:4].toDist, car[1:4].speed+tIter/2.f*k1[1:4], distance(car[1:4],car[0:4],car[1:4].speed+tIter/2.f*k1[1:4],car[0:4].speed+tIter/2.f*k1[0:4],tIter/2.f), tRealx);
k3[1:4] = speed(car[1:4].toSpeed, car[1:4].toDist, car[1:4].speed+tIter/2.f*k2[1:4], distance(car[1:4],car[0:4],car[1:4].speed+tIter/2.f*k2[1:4],car[0:4].speed+tIter/2.f*k2[0:4],tIter/2.f), tRealx);
k4[1:4] = speed(car[1:4].toSpeed, car[1:4].toDist, car[1:4].speed+tIter *k3[1:4], distance(car[1:4],car[0:4],car[1:4].speed+tIter *k3[1:4],car[0:4].speed+tIter *k3[0:4],tIter ), tRealx);
for(int i=1;i<5;i++){
float newSpeed = car[i].speed + (tIter/6)*(k1[i]+2*k2[i]+2*k3[i]+k4[i]);
car[i].y += tIter*car[i].speed + 0.5f*(newSpeed*newSpeed - car[i].speed*car[i].speed);
car[i].speed = newSpeed;
}
}
for(int i=1;i<5;i++){
printf("%f\t%f\t\t",car[i].y,car[i].speed);
}
printf("\n");
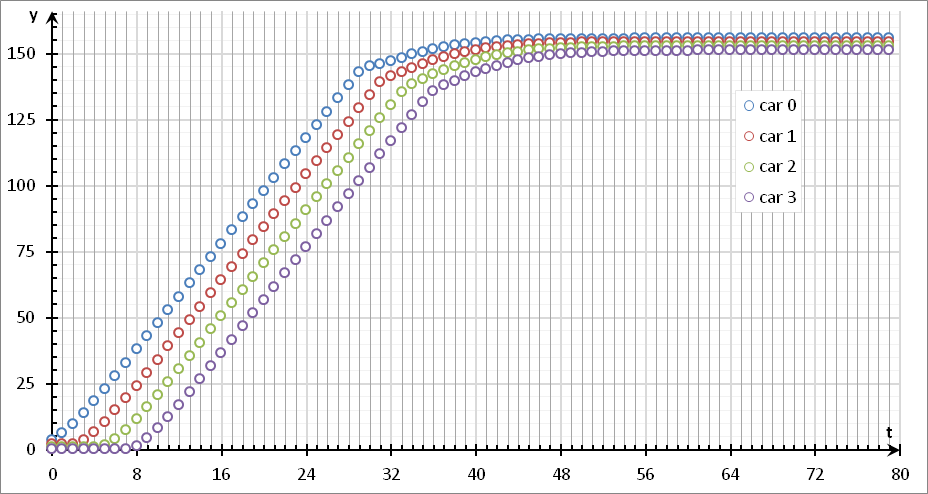
}
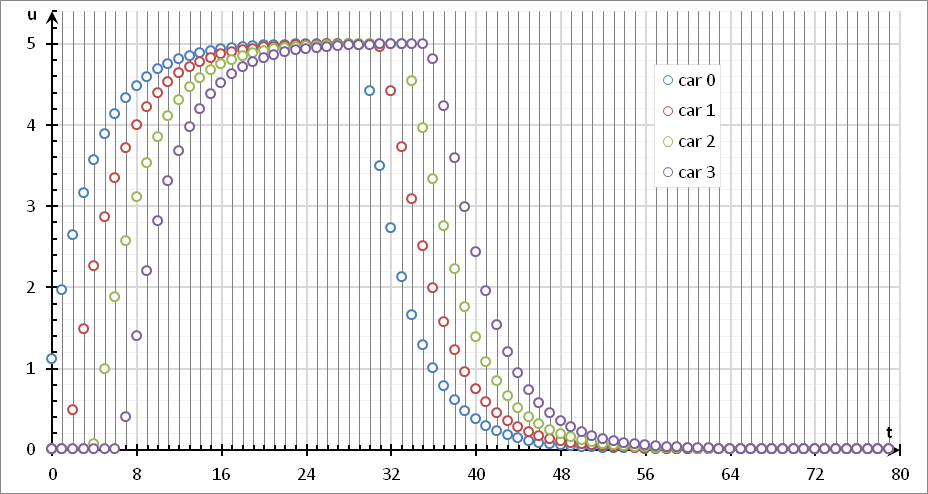
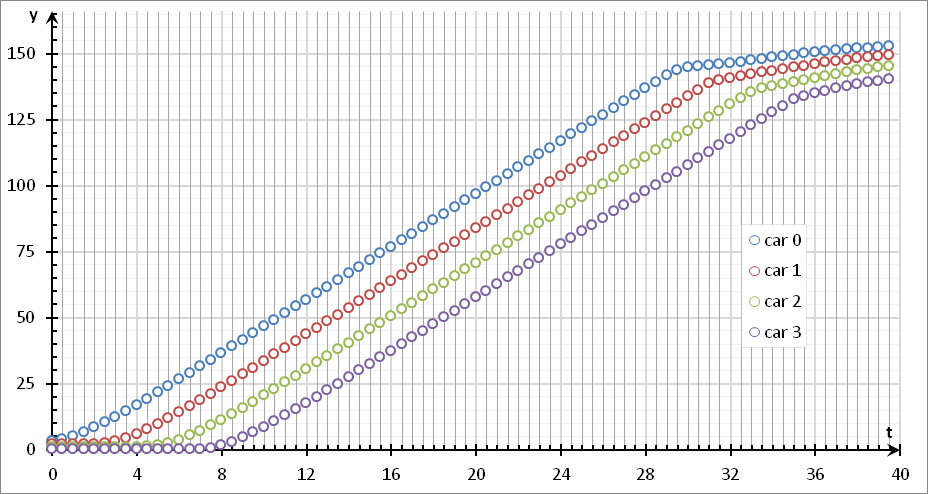
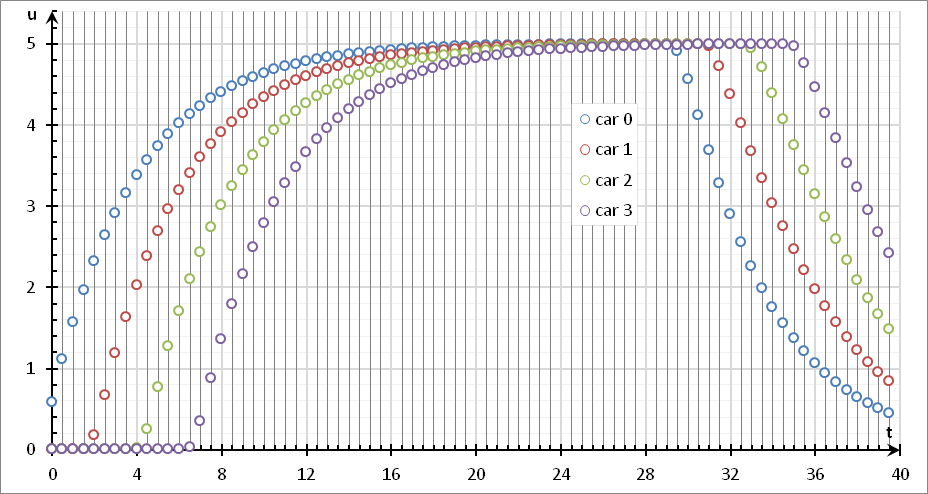
"Labs/Васильеву/calc"
-описание метрик и счетчиков процессора; -поиск узкого места методом "поиска темной кошки в темной комнате"; -внезапное решение (повезло, причина неясна - отсутствует счетчик в процессоре);
#include "approxmath.h"
// exp() is 1.092s
// tanhf() is 2.589s
#define A_EXP fast_exp
#define A_TANH rational_tanh
/*__declspec(align(16))*/
//struct Car{
// const float toSpeed = 5.f,
// toDist = 5.f,
// lenght = 1.f; // car: (end[lenght|y]>start)
// float y;
// float speed;
//};
__declspec(vector(uniform(tRealx)))
inline float speed(const float &toSpeed, const float &toDist, const float ¤tSpeed, const float ¤tDist, const float &tRealx)
{
return (1.f/tRealx)*(toSpeed/2.f*(A_TANH(currentDist-toDist)+A_TANH(toDist)) - currentSpeed);
}
__declspec(vector(uniform(tIter)))
inline float distance(const float &aSpeed, const float &aY, const float &bSpeed, const float &bY, const float &bLenght, const float &aNewSpeed, const float &bNewSpeed, const float &tIter)
{
return (bY-bLenght + tIter*bSpeed + 0.5f*(bNewSpeed*bNewSpeed - bSpeed*bSpeed)) - (aY + tIter*aSpeed + 0.5f*(aNewSpeed*aNewSpeed - aSpeed*aSpeed));
}
//speed-up x16
void calc_v2()
{
const float tRealx = 4.f;
const float tIter = 1.0f;
//Car car[5] = {{150.f,0.f}/*<-stop*/, {3.f,0.f}, {2.f,0.f}, {1.f,0.f}, {0.f,0.f}};
const float carToSpeed = 5.f,
carToDist = 5.f,
carLenght = 1.f;
__declspec(align(16)) float carSpeed[5] = {0.f /*<-stop*/, 0.f, 0.f, 0.f, 0.f};
__declspec(align(16)) float carY [5] = {150.f/*<-stop*/, 3.f, 2.f, 1.f, 0.f};
__declspec(align(16)) float carSpeed2[5] = {0.f /*<-stop*/, 0.f, 0.f, 0.f, 0.f};
__declspec(align(16)) float carY2 [5] = {150.f/*<-stop*/, 3.f, 2.f, 1.f, 0.f};
for(int iter=0; iter<80000; iter++){
__declspec(align(16)) float k1[5]={0.f}, k2[5]={0.f}, k3[5]={0.f}, k4[5]={0.f};
k1[1:4] = speed(carToSpeed, carToDist, carSpeed[1:4] , distance(carSpeed[1:4],carY[1:4],carSpeed[0:4],carY[0:4],carLenght,carSpeed[1:4] ,carSpeed[0:4] ,0.f ), tRealx);
k2[1:4] = speed(carToSpeed, carToDist, carSpeed[1:4]+tIter/2.f*k1[1:4], distance(carSpeed[1:4],carY[1:4],carSpeed[0:4],carY[0:4],carLenght,carSpeed[1:4]+tIter/2.f*k1[1:4],carSpeed[0:4]+tIter/2.f*k1[0:4],tIter/2.f), tRealx);
k3[1:4] = speed(carToSpeed, carToDist, carSpeed[1:4]+tIter/2.f*k2[1:4], distance(carSpeed[1:4],carY[1:4],carSpeed[0:4],carY[0:4],carLenght,carSpeed[1:4]+tIter/2.f*k2[1:4],carSpeed[0:4]+tIter/2.f*k2[0:4],tIter/2.f), tRealx);
k4[1:4] = speed(carToSpeed, carToDist, carSpeed[1:4]+tIter *k3[1:4], distance(carSpeed[1:4],carY[1:4],carSpeed[0:4],carY[0:4],carLenght,carSpeed[1:4]+tIter *k3[1:4],carSpeed[0:4]+tIter *k3[0:4],tIter ), tRealx);
//for speed-up x16 (51.458 / 3.125)
for(int i=1;i<5;i++){
float newSpeed = (tIter/6)*(k1[i]+2*k2[i]+2*k3[i]+k4[i]);
float newSpeed2 = carSpeed2[i] + newSpeed;
newSpeed += carSpeed[i];
carY[i] += tIter*carSpeed[i] + 0.5f*(newSpeed*newSpeed - carSpeed[i]*carSpeed[i]);
carSpeed2[i] = newSpeed -carSpeed [i]*1E-7f;
carSpeed [i] = newSpeed2-carSpeed2[i]*1E-7f;
}
}
for(int i=1;i<5;i++){
printf("%f\t%f\t\t",carY[i],carSpeed[i]);
}
printf("\n");
}
#include "approxmath.h"
// exp() is 1.092s
// tanhf() is 2.589s
#define A_EXP fast_exp
#define A_TANH rational_tanh
#include "../OverSpeedGPU/gpu.cuh"
/*__declspec(align(16))*/
//struct Car{
// const float toSpeed = 5.f,
// toDist = 5.f,
// length = 1.f; // car: (end[length|y]>start)
// float y;
// float speed;
//};
__declspec(vector(uniform(tRealx)))
inline float speed(const float toSpeed, const float toDist, const float currentSpeed, const float currentDist, const float tRealx)
{
return (1.f/tRealx)*(toSpeed/2.f*(A_TANH(currentDist-toDist)+A_TANH(toDist)) - currentSpeed);
}
__declspec(vector(uniform(tIter)))
inline float distance(const float aSpeed, const float aY, const float bSpeed, const float bY, const float bLength, const float aNewSpeed, const float bNewSpeed, const float tIter)
{
return (bY-bLength + tIter*bSpeed + 0.5f*(bNewSpeed*bNewSpeed - bSpeed*bSpeed)) - (aY + tIter*aSpeed + 0.5f*(aNewSpeed*aNewSpeed - aSpeed*aSpeed));
}
//speed-up x16
void calc_v2()
{
const float tRealx = 4.f;
const float tIter = 1.0f;
const float carToSpeed = 5.f,
carToDist = 5.f,
carLength = 1.f;
struct aln16float4bef4{float stop[4]; __declspec(align(16)) float a[4];};
__declspec(align(64)) struct{
aln16float4bef4 Speed;// = {{}, {}};
aln16float4bef4 Y;// = {{0.f, 0.f, 0.f, 150.f/*<-stop*/}, {3.f, 2.f, 1.f, 0.f}};
aln16float4bef4 k1, k2, k3, k4;
aln16float4bef4 Speed2;//= {{}, {}};
} car = {{{},{}}, {{0.f, 0.f, 0.f, 150.f/*<-stop*/}, {3.f, 2.f, 1.f, 0.f}}, {},{},{},{}, {{},{}}};
#define calcK(tIter, pervK, pervKB) speed(carToSpeed, carToDist, car.Speed.a[:]+(tIter)*(pervK), distance(car.Speed.a[:],car.Y.a[:],car.Speed.a[-1:4],car.Y.a[-1:4],carLength,car.Speed.a[:]+(tIter)*(pervK),car.Speed.a[-1:4]+(tIter)*(pervKB),(tIter)), tRealx);
for(int iter=0; iter<800000; iter++){
car.k1.a[:] = calcK(0.f, 0.f, 0.f);
car.k2.a[:] = calcK(tIter/2.f, car.k1.a[:], car.k1.a[-1:4]);
car.k3.a[:] = calcK(tIter/2.f, car.k2.a[:], car.k2.a[-1:4]);
car.k4.a[:] = calcK(tIter, car.k3.a[:], car.k3.a[-1:4]);
//for speed-up x16 (51.458 / 3.125)
for(int i=0;i<4;i++){
float newSpeed = (tIter/6.f)*(car.k1.a[i]+2.f*car.k2.a[i]+2.f*car.k3.a[i]+car.k4.a[i]);
float newSpeed2 = car.Speed2.a[i] + newSpeed;
newSpeed += car.Speed.a[i];
car.Y.a[i] += tIter*car.Speed.a[i] + 0.5f*(newSpeed*newSpeed - car.Speed.a[i]*car.Speed.a[i]);
car.Speed2.a[i] = newSpeed -car.Speed .a[i]*1E-7f;
car.Speed .a[i] = newSpeed2-car.Speed2.a[i]*1E-7f; // "-car.Speed2.a[i]*1E-7f" for stabilize (can be deleted)
}
}
#undef calcK
for(int i=0;i<4;i++){
printf("%f\t%f\t\t",car.Y.a[i],car.Speed.a[i]);
}
printf("\n");
}В модели 2 изолированные дороги, на каждой дороге по 4 автомобиля. Результат: линейное ускорение в 2 раза (по числу ядер - 2 ядра).
int main()
{
#if !true
cilk_spawn calc_v2();
cilk_spawn calc_v2();
#else
#pragma omp parallel sections
{
#pragma omp section
calc_v2();
#pragma omp section
calc_v2();
}
#endif
return 0;
}Графики нагрузки на CPU, графики накладных расходов при использовании OpenMP и Cilk Plus, ...
-что позволило еще увеличить производительность (указатели, описание формата файла - pxe - каждое выражение создает новую переменную -> оптимизация излишне); -игры с заменой проверки условия на вычисление без проверки условия (на CPU и GPU) на множестве исходных данных; -статья (en, pdf) про про минимизацию простоя при проверке условия на GPU ("Принцип тетриса" Reducing Branch Divergence in GPU Programs [http://www.ece.neu.edu/groups/nucar/GPGPU4/files/han.pdf]).
Конфигурация модели: количество автомобилей на одной дороге - 32; клоичество изолированных дорог - 864; всего автомобилей - (32X8)x(4x27) = 27 648.
#include "cuda_profiler_api.h"
#include "gpu.cuh"
#include "../OverSpeed/approxmath.h"
// exp() is 1.092s
// tanhf() is 2.589s
#define A_EXP fast_exp
#define A_TANH rational_tanh
#define WARP_SIZE_X 32
#define BLOCK_SIZE_Y 8
__device__ __forceinline__
float speed(const float toSpeed, const float toDist, const float currentSpeed, const float currentDist, const float tRealx)
{
return (1.f/tRealx)*(toSpeed/2.f*(A_TANH(currentDist-toDist)+A_TANH(toDist)) - currentSpeed);
}
__device__ __forceinline__
float distance(const float aSpeed, const float aY, const float bSpeed, const float bY, const float bLength, const float aNewSpeed, const float bNewSpeed, const float tIter)
{
return (bY-bLength + tIter*bSpeed + 0.5f*(bNewSpeed*bNewSpeed - bSpeed*bSpeed)) - (aY + tIter*aSpeed + 0.5f*(aNewSpeed*aNewSpeed - aSpeed*aSpeed));
}
__global__ void calc_vGPU(float *__restrict__ _SpeedLog_, float *__restrict__ _YLog_)
{
const float tRealx = 4.f;
const float tIter = 1.0f;
const float carToSpeed = 5.f,
carToDist = 5.f,
carLength = 1.f;
__shared__ float _CarSpeed[BLOCK_SIZE_Y][WARP_SIZE_X+1];
__shared__ float _CarY [BLOCK_SIZE_Y][WARP_SIZE_X+1];
__shared__ float _PervK [BLOCK_SIZE_Y][WARP_SIZE_X+1];
// "volatile" required for correct calculation!
volatile float *const _tCarSpeed = &_CarSpeed[threadIdx.y][threadIdx.x+1];
volatile float *const _tCarY = &_CarY [threadIdx.y][threadIdx.x+1];
volatile float *const _tPervK = &_PervK [threadIdx.y][threadIdx.x+1];
float carSpeed = 0.f;
float carY = WARP_SIZE_X - threadIdx.x - 1;
float k1, k2, k3, k4;
_tCarSpeed [-1] = 0.f;
if(threadIdx.x != 0){
_tCarY [-1] = WARP_SIZE_X - threadIdx.x;
} else {
_tCarY [-1] = 150.f;/*<-stop*/
_tPervK[-1] = 0.f;
}
#define calcK(tIter, pervK, pervKB) speed(carToSpeed, carToDist, carSpeed+(tIter)*(pervK), distance(carSpeed,carY,carSpeedB,carYB,carLength,carSpeed+(tIter)*(pervK),carSpeedB+(tIter)*(pervKB),(tIter)), tRealx)
for(int iter=0; iter<800000; iter++){
const float carSpeedB = _tCarSpeed[-1];
const float carYB = _tCarY [-1];
_tPervK[0] = k1 = calcK(0.f, 0.f, 0.f);
_tPervK[0] = k2 = calcK(tIter/2.f, k1, _tPervK[-1]);
_tPervK[0] = k3 = calcK(tIter/2.f, k2, _tPervK[-1]);
k4 = calcK(tIter, k3, _tPervK[-1]);
const float newSpeed = carSpeed + (tIter/6.f)*(k1 + 2.f*k2 + 2.f*k3 + k4);
carY += tIter*carSpeed + 0.5f*(newSpeed*newSpeed - carSpeed*carSpeed);
carSpeed = newSpeed;
_tCarSpeed[0] = newSpeed;
_tCarY [0] = carY;
}
#undef calcK
_SpeedLog_[((blockIdx.y*gridDim.x + blockIdx.x)*blockDim.y + threadIdx.y)*blockDim.x + threadIdx.x] = carSpeed;
_YLog_ [((blockIdx.y*gridDim.x + blockIdx.x)*blockDim.y + threadIdx.y)*blockDim.x + threadIdx.x] = carY;
}
float calc_vGPU_proxy()
{
cudaSetDeviceFlags(cudaDeviceScheduleBlockingSync | cudaDeviceMapHost);
{
const dim3 blocksNum = dim3(32/BLOCK_SIZE_Y /*-1*/, 27, 1);
const size_t threadsNum = blocksNum.x*blocksNum.y*WARP_SIZE_X*BLOCK_SIZE_Y;
float *hostSpeedLog, *hostYLog;
cudaMallocHost(&hostSpeedLog, sizeof(float)*threadsNum, cudaHostAllocMapped);
cudaMallocHost(&hostYLog, sizeof(float)*threadsNum, cudaHostAllocMapped);
//cudaHostAlloc
float *devSpeedLog, *devYLog;
cudaHostGetDevicePointer(&devSpeedLog, hostSpeedLog, 0U);
cudaHostGetDevicePointer(&devYLog, hostYLog, 0U);
{
cudaStream_t stream;
cudaStreamCreateWithFlags(&stream, cudaStreamNonBlocking);
cudaProfilerStart();
calc_vGPU<<<blocksNum,dim3(WARP_SIZE_X, BLOCK_SIZE_Y, 1),0,stream>>>(devSpeedLog, devYLog);
cudaProfilerStop();
cudaStreamSynchronize(stream);
cudaStreamDestroy(stream);
}
for(int i=0;i<threadsNum;i++) printf("%f\t%f\n", hostSpeedLog[i] ,hostYLog[i]);
cudaFreeHost(hostYLog);
cudaFreeHost(hostSpeedLog);
}
cudaDeviceReset();
return 0.f;
}(Однопоточный вариант) CPU x16; (Многопоточный) CPU + x2 (у меня 2 ядра); GPU x14.4 (от многопоток. CPU) -> (еще раз ускорил версию для CPU и GPU) -> GPU x17.467.
Сравнение скорости работы версии для CPU с версией для GPU: Вначале версия для GPU была в 14.4 раз быстрее версии для CPU. Затем была использована еще одна оптимизация для обеих версий, и в итоге расчет 800 000 итераций: на CPU (количество автомобилей: 4x2 = 8; количество дорог: 2) занял 30.833 мс; на GPU (количество автомобилей: (32X8)x(4x27) = 27 648; количество дорог: 864) занял 6100.598 мс. Если предположить, что зависимость времени расчета от числа автомобилей - линейная (хотя это не верно), то расчет 800 000 итераций на CPU (количество автомобилей: (32x8)x(4x27) = 27 648; количество дорог: 864) длился бы 30.833*32*4*27 = 106558.848 мс. В итоге получаем соотношение tCPU / tGPU = 106558.848/6100.598 = 17.467
Добро пожаловать в раннюю версию Brackets, нового редактора с открытым исходным кодом для веба следующего поколения. Мы большие фанаты стандартов и хотим построить лучший инструмент для JavaScript, HTML и CSS и связанных с ними открытых веб-технологий. Это наше скромное начало.